Phase, Phase angle, phase difference, ഫേസ്, ഫേസ്ഡിഫറൻസ്

വെക്ടറും സ്കെയ്‌ലാറും പിന്നൊരു ഫേസും. ( Vector, scalar and phase )

വൈദ്യുതിയുമായി ബന്ധപ്പെട്ട്‌ എല്ലായ്പ്പോഴുമെന്ന പോലെ ഉപയോഗിയ്ക്കുന്ന പദമാണ്‌ ഫേസ്‌ ( Phase ) എന്നത്‌. ത്രീ ഫേസ്‌ ( Three phase ), സിംഗിൾ ഫേസ്‌ (Single phase ) മുതലായ പദങ്ങൾ ധാരാളമായി പറയപ്പെടുന്നവയാണ്‌. ഒരു വൈദ്യുത കണക്ഷണപേക്ഷിയ്ക്കുമ്പോൾ പോലും സിംഗിൾ ഫേസ്‌ വേണോ ത്രീ ഫേസ്‌ വേണോ എന്ന ചോദ്യം ഉയരും. മാത്രമല്ല കൂടുതലായി പഠിയ്ക്കുന്ന വേളയിലാകട്ടെ ഫേസ്‌ ഡിഫറൻസ്‌ ( Phase difference ), ഫേസ്‌ ആംഗിൾ (Phase angle) തുടങ്ങിയങ്ങോട്ടു ഫേസിന്റെ ഒരു പൂരം തന്നെ കാണാം. അപ്പോൾ എന്താണീ ഫേസ്‌? പണ്ടുതൊട്ടേ ഒരു കീറാമുട്ടിയാണീ ഫേസും ഫേസ്‌ ഡിഫറൻസുമൊക്കെ. ഇത്ര വല്യ പുള്ളിയാണെങ്കിൽ അവനെ ത്തന്നെ അങ്ങു പിടിച്ചേക്കാം എന്നു വിചാരിച്ചു ഫേസിനെക്കുറിച്ചു ഞാനറിഞ്ഞ കാര്യങ്ങൾ ഒന്നങ്ങോട്ടെഴുതുകയാണ്‌.

വെക്ടറും സ്കയ്‌ലാറും ( Vector and scalar )

അളവുകൾ ( Quantities )

നമ്മുടെ നിത്യ ജീവിതത്തിൽ നാം ധാരാളം അളവുകൾ ( Measurements) നടത്താറുണ്ട്‌. സാങ്കേതികപരമായ കാര്യങ്ങളിലാണെങ്കിലോ അളവില്ലാതൊന്നുമില്ല. ആളുകളുടെ പൊക്കം, വണ്ണം, പറമ്പിന്റെ വിസ്തീർണ്ണം, വീടിന്റെ വിസ്തീർണ്ണം, സമയം തുടങ്ങി ഒട്ടനേകം കാര്യങ്ങൾ അളക്കുന്നുണ്ട്‌. ഇപ്പോഴാണെങ്കിൽ പണ്ടത്തേതിനേക്കാൾ ഒന്നു കൂടെയുണ്ട്‌- മൊബൈൽ ഡാറ്റ അതില്ലാതെ ഇപ്പൊ ജീവിതം തന്നെയില്ലാല്ലോ. അതെന്തായാലും ഒരോ അളവുകൾക്കും ( Quantities ) അതിന്റേതായ അളവു രീതികൾ ( Measuring methods), അളവുപകരണങ്ങൾ ( Measuring instruments ), ഏകകങ്ങൾ( Units) എന്നിവയുണ്ടാകും. വൈദ്യുതിയുമായി ബന്ധപ്പെട്ടാകട്ടെ വോൾട്ടത (Voltage), പ്രവാഹ തീവ്രത (Current), വൈദ്യുത ശക്തി (Power), വൈദ്യുതോർജ്ജം (Energy), താപനില (Temperature), എന്നിവയും വൈദ്യുതോപകരണങ്ങൾക്ക്‌ വേഗത, വിറയൽ (vibration) എന്നിങ്ങനെ പലതും അളക്കേണ്ടതത്യാവശ്യമാണ്‌.

എല്ലാത്തരം അളവുകളും ഒരുപോലെയാണോ? അല്ല,  ചില അളവുകൾക്കു ഋണമൂല്യമുണ്ടാകില്ല ( Negative value ) ,ധനമൂല്യം ( Positive value ) മാത്രമേ സാധുവാകൂ, ഉദാഹരണം നീളം ( length ), വിസ്തീർണ്ണം ( area ) മുതലായവ. ചിലവയ്ക്കാണെങ്കിലോ ഇതു രണ്ടുമാകാം. ഉദാഹരണത്തിനു താപനില പൊടെൻഷ്യൽ മുതലായവ.

ആധാരങ്ങൾ ( References )

എപ്രകാരമാണു അളവുകൾക്ക്‌ ധന ഋണ മൂല്യങ്ങളുണ്ടാകുന്നത്‌.

എല്ലാ അളവുകളും ആപേക്ഷികമാണ്‌. നിശ്ചിതമായ ഒരു ആധാരത്തെ (Reference) അടിസ്ഥാനമാക്കി മാത്രമേ അളവുകൾ സാധ്യമാകൂ. ഉദാഹരണത്തിനു നാം ഒരാളുടെ ഉയരം അളക്കുകയാണെങ്കിൽ അയാളെ തറയിൽ നിർത്തിയശേഷം പാദം മുതൽ ശിരസ്സു വരെ ടേപ്പോ മുഴക്കോലോ മറ്റോ ഉപയോഗിച്ചളക്കുന്നു. ഇവിടെ തറ പൂജ്യം എന്ന മൂല്യത്തിൽ കണക്കാക്കിയാണു നാം അളക്കുന്നത്‌. അതു കൊണ്ട്‌ തറയുടെ അളവാണിവിടെ ആധാരം. അതായത്‌ തറയിൽ നിന്നും അല്ലെങ്കിൽ കാൽ മുതൽ തല വരെ ഇത്ര മീറ്റർ ഉയരം എന്നാണു പ്രസ്താവിയ്ക്കുന്നത്‌. അതുപോലെ നീളം, ഏതെങ്കിലുമൊരു ബിന്ദുവിനെ ആധാരമാക്കിക്കൊണ്ടാണളക്കുന്നത്‌. സമയം, താപനില മുതലായവയൊക്കെ അങ്ങിനെ തന്നെ. 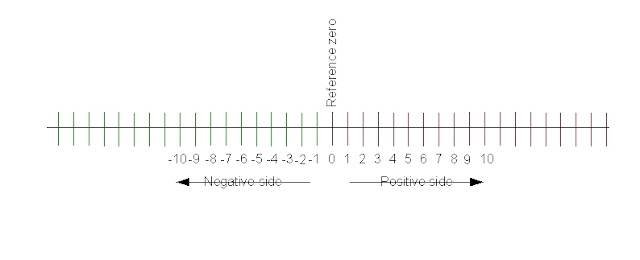എല്ലാ അളവുകളിലും (measurements) പൂജ്യത്തെ ആധാരമാക്കിക്കൊണ്ടാണ്‌ നാം അളക്കുന്നത്‌. അല്ലെങ്കിൽ നമ്മുടെ ആധാരത്തിന്റെ മൂല്യം പൂജ്യമാണെന്നു സങ്കൽപ്പിയ്ക്കുന്നു. ചിത്രം കാണുക.

നീളം (length), സമയം (time), പിണ്ഡം (mass) എന്നിവയാണു മൂന്നു അടിസ്ഥാന അളവുകൾ (quantities). ഇതിൽ ഒരു വസ്തുവിന്റെ നീളം ( ഉയരം, വണ്ണം, വിസ്തീർണ്ണം, ഘനം), പിണ്ഡം എന്നിവ ഋണ മൂല്യമുള്ളതാകാൻ (negative value ) സാധിയ്ക്കയില്ല. ഒരു വസ്തുവിന്റെ ഉയരം -10 സെ.മി. എന്നതൊരു അർത്ഥശൂന്യമായ പ്രസ്താവനയാണല്ലോ. ആയതുകൊണ്ടു തന്നെ അവയുടെയൊക്കെ ആധാരം (Reference) ഏറ്റവും കുറഞ്ഞ മൂല്യത്തിലായിരിയ്ക്കും. എന്നാൽ സമയം, താപനില എന്നിവയ്ക്കൊക്കെ പൂജ്യത്തിനും പിറകിലേയ്ക്കു അളക്കുക സാധ്യമാണ്‌. കാശ്മീരിലെ ഇന്നത്തെ ഊഷ്മാവ്‌ -10 ഡിഗ്രിയെന്നു പലപ്പോഴും വാർത്തകളിൽ വരുന്നതാണല്ലോ. അപ്പോ ചില അളവുകൾക്കു ഋണമൂല്യം സാധ്യമാണ്‌. ചിത്രം കാണുക. (ഇങ്ങനെ ഋണ മൂല്യം കിട്ടുന്നത്‌ യഥാർത്ഥത്തിൽ ആധാരം നിർണ്ണയിയ്ക്കുന്ന രീതികാരണമാണ്‌. കൃത്യമായി ഒരു പൂജ്യം ആധാരത്തിലെത്താൻ പറ്റാതിരിയ്ക്കുമ്പോൾ അളവുശ്രേണിയിലെ സൗകര്യപ്രദമായ ഒരു സ്ഥാനം ആധാരമായി സങ്കൽപ്പിയ്ക്കുന്നു. എന്നിട്ടതിനു പൂജ്യമെന്ന മൂല്യം നൽകി അവിടെനിന്നും ധന വശത്തേയ്ക്കും ( positive side ) ഋണ വശത്തേയ്ക്കും  (negative side) അളക്കുന്നു. നമ്മുടെ സംഖ്യാശ്രേണി പോലെ. അല്ലെങ്കിൽ സമയം അളക്കുന്നപോലെ. ദിവസം ആരംഭിയ്ക്കുന്ന അർദ്ധരാത്രിയെ പൂജ്യം സമയമാക്കി കണക്കാക്കി അവിടെനിന്നും ഒരു മണി, രണ്ടുമണി എന്നിങ്ങനെ പോകും. അർദ്ധരാതിയിൽ നിന്നും പിറകോട്ടും അതുപോലെ അളന്നു പോകാമല്ലോ. അപ്പോൾ എല്ലാത്തരം അളവുകളും ഒരു ആധാരത്തെ ആസ്പദമാക്കി മാത്രമേ നടത്താൻ സാധിയ്ക്കൂ എന്നു മനസ്സിലായി.

സ്കെയ്‌ലാർ അളവുകൾ ( scalar quantities )

ചില അളവുകൾ പ്രസ്താവിയ്ക്കുമ്പോൾ അതിന്റെ മൂല്യം ( magnitude ) മാത്രം പ്രസ്താവിച്ചാൽ തന്നെ അതു പൂർണ്ണമാകും. ഉദാഹരണം ഊഷ്മാവ്‌ 10 ഡിഗ്രിയെന്നു പറഞ്ഞാൽ അല്ലെങ്കിൽ -10 ഡിഗ്രിയെന്നു പറഞ്ഞാൽ ആ പ്രസ്താവന പൂർണ്ണമാകുകയും അവയുടെ മൂല്യത്തെ (magnitude)  കണക്കുകൂട്ടലുകളിൽ നേരിട്ടുപയോഗിയ്ക്കാൻ സാധിയ്ക്കുകയും ചെയ്യും.. ഇങ്ങനെ ലഘുവായി മൂല്യം മാത്രം പ്രസ്താവിയ്ക്കാൻ കഴിയുന്ന അളവുകളെ സ്കെയ്‌ലാർ അളവുകൾ ( scalar quantities )എന്നു പറയുന്നു. ഉദാഹരണത്തിനു നീളം ( length ), സമയം ( Time ), പിണ്ഡം( mass ), വേഗം ( speed ), മുതലായവ

വെക്ടർ അളവുകൾ ( Vector quantintes )

ചില അളവുകൾ പ്രസ്താവിയ്ക്കുമ്പോൾ  അവയുടെ മൂല്യം ( magnitude ) മാത്രം പ്രസ്താവിച്ചാൽ പൂർണ്ണമാകില്ല. ഉദാഹരണം ബലം ( force ), ബലത്തിനൊരു നിശ്ചിതമായ മൂല്യമുണ്ടായിരിയ്ക്കും, മാത്രമല്ല ഒരു നിശ്ചിത ദിശയും ( Direction ) ഉണ്ടായിരിയ്ക്കും. ഉദാഹരണത്തിനു ഒരാളെ മറ്റൊരാൾ പിടിച്ചു തള്ളുകയാണെങ്കിൽ ആ തള്ളിനൊരു ശക്തിയുണ്ടാകുമെന്നു മാത്രമല്ല ഒരു ദിശയുമുണ്ടാകുമല്ലോ , കാരണം ആ തള്ളിന്റെ ദിശയിലായിരിയ്ക്കും അയാൾ  തെറിച്ചുപോകുക. അപ്പോൾ ഇത്തരം അളവുകളിൽ മൂല്യം ( magnitude )  മാത്രമളന്നാൽ പോരാ അവയുടെ ദിശകൂടി നിർബന്ധമായും പരാമർശിയ്ക്കേണ്ടി വരും.  അല്ലാത്തപക്ഷം ആ അളവിനെ കണക്കുകൂട്ടലുകളിൽ ഉപയോഗിയ്ക്കാൻ പറ്റില്ല. ഇത്തരത്തിൽ മൂല്യത്തോടൊപ്പം ദിശയും പ്രസ്താവിയ്ക്കേണ്ട അളവുകളെയാണൂ വെക്ടർ അളവുകൾ എന്നു പറയുന്നത്‌. ഉദാഹരണം – ബലം (Force), വൈദ്യുത പൊട്ടൻഷ്യൽ (Electric Potential), പ്രവേഗം (Velocity), അനുനിമിഷ കരണ്ട്‌, വോൾട്ടേജ്‌ (Instantaneous current & Voltage) മുതലായവ.

അതായത്‌ വെക്ടർ അളവുകൾ പ്രസ്താവിയ്ക്കുമ്പോൾ അവയുടെ മൂല്യത്തോടൊപ്പം ( Magnitude ) അവ അനുഭവപ്പെടുന്ന ദിശയും ( Direction ) പ്രഖ്യാപിയ്ക്കേണ്ടതുണ്ട്‌. എങ്കിലേ വെക്ടർ അളവുകൾ പൂർണ്ണമാകൂ.

സ്കയ്‌ലാർ അളവുകളെ അവയുടെ മൂല്യം കൊണ്ടു മാത്രം പ്രസ്താവിയ്ക്കാൻ കഴിയും. അതിനാൽ അവയ്ക്ക്‌ രേഖീയമായ ഒരു പ്രതിനിധീകരണം (Graphical representation) ആവശ്യമില്ല. എന്നാൽ വെക്ടറുകളെ ദിശയടക്കം പ്രഖ്യാപിയ്ക്കുന്നതിനാൽ അവയെ ഗണിതപരമായ രൂപത്തിലും (Mathematical form) രേഖീയമായ രൂപത്തിലും ( Graphical form ) പ്രതിനിധീകരിയ്ക്കാൻ സാധിയ്ക്കും. മാത്രമല്ല  രേഖീയമായ പരമായി അവയുടെ കണക്കുകൂട്ടലുകളും നടത്തുവാൻ സാധിയ്ക്കും.

വെക്ടറുകളും ദിശയും. ( Vectors and their Directions )

വെക്ടറായാലും സ്കയ്‌ലാറായലും അളവുകളുടെ മൂല്യം ( Magnitude ) സംഖ്യ കളായി ഗണിതരൂപത്തിൽ രേഖപ്പെടുത്താം. എന്നാൽ എപ്രകാരമാണ്‌ ദിശയു ണ്ടാകുന്നതും അതു രേഖപ്പെടുത്തുന്നതും. ചിത്രം കാണുക.

ഇവിടെ കാണിച്ചിട്ടുള്ള കുറ്റിയിൽ കെട്ടിയിട്ടുള്ള കയറിനെ വലത്തോട്ടു വലിയ്ക്കുകയാണ്‌. നിശ്ചിതമായ അളവിലുള്ള ബലമാണ്‌ കയറുവഴി ആ കുറ്റിയിൽ പ്രയോഗിയ്ക്കപ്പെടുന്നത്‌. ആ കുറ്റിയിന്മേലനുഭവപ്പെടുന്ന ബലം വലതു ദിശയിലേയ്ക്കാണെന്നു നമുക്കറിയാം. അപ്പോൾ വലതു ദിശയാണ്‌ ആ ബലത്തിന്റെ ദിശ. അതുപോലെ ഒരു വസ്തുവിലോ കുറ്റിയിലോ പ്രയോഗിയ്ക്കപ്പെടുന്ന ബലത്തിന്റെ ദിശ അറിയാമല്ലോ, കാരണം അ ദിശയിലായിരിയ്ക്കും വസ്തുവിനു സ്ഥാനാന്തരണമുണ്ടാകുക. ഇതുപോലെ തന്നെ മറ്റു വെക്ടർ അളവുകളുടേയും  ദിശ നമുക്കു കാണാവുന്നതാണ്‌.

എന്നാൽ ഇപ്രകാരം ദിശ നമുക്കറിയാമെങ്കിലും എപ്രകാരം അവയെ പ്രതിനിധീകരിയ്ക്കും?, അവയെ ഗണിതക്രിയകളിലുപയോഗിയ്ക്കും? അങ്ങനെ പ്രതിനിധീകരിച്ചതുകൊണ്ടല്ലേ അവ അളക്കുന്നതുകൊണ്ടു പ്രയോജനമുള്ളൂ. 10 ന്യൂട്ടൺ ബലം വലത്തേയ്ക്കു, അല്ലെങ്കിൽ 20 ന്യൂട്ടൺ ബലം മേലോട്ട്‌ എന്നൊക്കെ പറയാമെങ്കിലും അത്‌ ഗണിതക്രിയയ്ക്കനുയോജ്യമല്ല, കാരണം എല്ലാ ബലങ്ങളും വലത്തോട്ടോ ഇടത്തോട്ടോ അല്ലെങ്കിൽ ഏതാനും ചില ദിശകളിലോ മാത്രമല്ല പ്രയോഗത്തിൽ വരുന്നത്‌ ( മറ്റു വെക്ടറുകളും ). ഈ പ്രശ്നം പരിഹരിയ്ക്കാൻ വിവരമുള്ളവർ ചില മാർഗ്ഗങ്ങൾ കണ്ടുപിടിച്ചിട്ടുണ്ട്‌. അവ താഴെ കാണും വിധം ക്രോഡീകരിയ്ക്കാം.

1,  രേഖാ ചിത്ര പ്രതിനിധീകരണം. ( Graphical representation )

താരതമ്യേന എളുപ്പമുള്ളതും കണ്ടാൽ എളുപ്പം മനസ്സിലാക്കാവുന്നതുമായ ഒരു രീതിയാണിത്‌. വെക്ടറുകളെ ഒരു ഗ്രാഫ്‌ ഷീറ്റിൽ വരയ്ക്കുന്നു. വെക്ടറുകളുടെ മൂല്യം ഗ്രാഫ്‌ കടലാസിൽ ആനുപാതികമായി രേഖപ്പെടുത്തുന്നു. എന്നാൽ അവയുടെ ദിശയും ( Direction )കൂടി പരിഗണിച്ചുകൊണ്ടാണിത്‌ ചെയ്യുക. വെക്ടറുകളെ ഒരു രേഖയായിട്ടാണു ഗ്രാഫിൽ വരയ്ക്കുക. വെക്ടറുകളുടെ മൂല്യത്തിനാനുപാതികമായിരിയ്ക്കും ഈ രേഖയുടെ നീളം. അവയുടെ ദിശ കോണിയ ( Angular ) അളവായി രേഖപ്പെടുത്തി ആ കോണളവിലായിരിയ്ക്കും രേഖ വരയ്ക്കുക.

ഗ്രാഫിൽ വരയ്ക്കുമ്പോൽ X അക്ഷവും Y അക്ഷവുമുണ്ടല്ലോ. X  അക്ഷത്തിന്റെ കോണളവ്‌ പൂജ്യമായി സങ്കൽപ്പിച്ച്‌ അതിനെ ആധാരമാക്കിയാണ്‌ ( Reference ) എല്ലാ കോണളവുകളും കണക്കാ‍ക്കുന്നത്‌. ഉദാഹരണത്തിനു 30 ഡിഗ്രി ദിശയുള്ള ഒരു വെക്ടറിനെ താഴെ കാണും വിധ ഗ്രാഫിൽ പ്രതിനിധീകരിയ്ക്കാം.

വെക്ടറുകളുടെ ഗണിതക്രിയ ഗ്രാഫിൽ

ഒരേ വസ്തുവിൽ രണ്ടു ബലം പ്രവർത്തിയ്ക്കുന്നെന്നു കരുതുക. താഴെ ചിത്രം കാണുക.

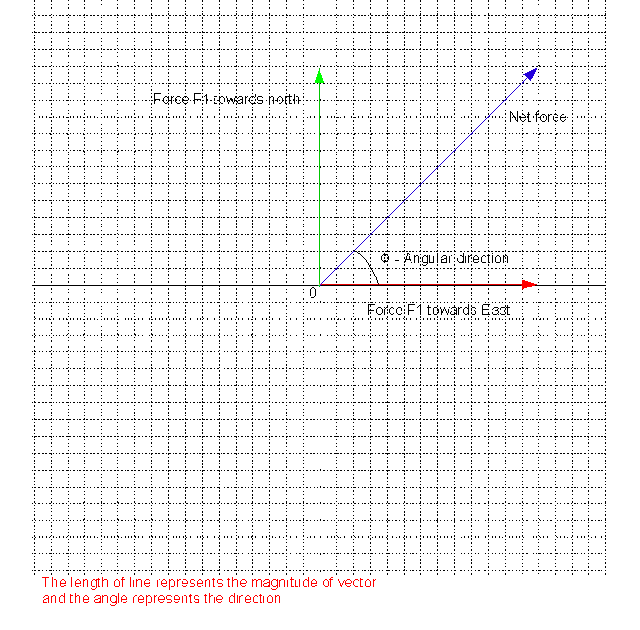
ഒരു കുറ്റിയിൽ രണ്ടു കയറുകളുപയോഗിച്ച്‌ ഒന്നിനെ വടക്കോട്ടും മറ്റൊന്നുകൊണ്ട്‌ കിഴക്കോട്ടും വലിയ്ക്കുന്നു. കുറ്റി എങ്ങോട്ടു ചെരിയും. ബലങ്ങൾ രണ്ടും തുല്യമാണെങ്കിൽ അത് വടക്കു കിഴക്കു ദിശയിലേയ്കായിരിയ്ക്കും എന്നനുമാനിയക്കാം. ഇനി രണ്ടും തുല്യ ബലമല്ലെങ്കിലോ വടക്കുകിഴക്കെ ദിക്കിലായിരിയ്ക്കയില്ലാ അതിന്റെ ദിശ അവിടെ നിന്നും ബലം കൂടിയ ദിശയിലേയ്ക്കൽപ്പം മാറിയായിരിയ്ക്കില്ലേ കുറ്റിയിലനുഭവപ്പെടുന്ന  ബലത്തിന്റെ ദിശ. മാത്രമല്ല. കുറ്റിയിലനുഭവപ്പെടുന്ന ആകെ ബലമെത്രയായിരിയ്ക്കും. ഒന്നാമത്തെയും രണ്ടാമത്തേയും ബലങ്ങളുടെ മുല്യങ്ങൾ തമ്മിൽ കൂട്ടിയാൽ കിട്ടുന്നതായിരിയ്ക്കില്ല സഫല ( net ) ബലത്തിന്റെ മൂല്യം. അപ്പോളിതെങ്ങിനെ കണ്ടുപിടിയ്ക്കാം? രേഖാചിത്ര പ്രതിനിധീകരണത്തിലൂടെ ( graphical representation ) ഇത്‌  എളുപ്പാം കണ്ടുപിടിയ്ക്കാവുന്നതേയുള്ളൂ. താഴെ ഗ്രാഫ്‌ ശ്രദ്ധിയ്ക്കുക. കുറ്റിയിൽ പ്രയോഗിച്ച്‌ രണ്ടു ബലങ്ങളും ഗ്രാഫിൽ കാണിച്ചിരിയ്ക്കുന്നു. അവയുടെ അറ്റ  ബലമെന്നത്‌ ഗ്രാഫിൽ കാണിച്ചിരിയ്ക്കുന്നു.

ബലങ്ങളുടെ സംയോജന നിയമം.

 ഒരു വസ്തുവിലോ ബിന്ദുവിലോ പ്രയോഗിയ്ക്കപ്പെടുന്ന ബലങ്ങളെ ഒരു സാമാന്തരികത്തിന്റെ ( Parallelogram ) ഇരു സമീപ വശങ്ങളുടെ രൂപത്തിൽ പ്രതിനിധീകരിയ്ക്കാൻ സാധിയ്കുമെങ്കിലവയുടെ തുകയെ ആ സാമാന്തരികത്തിന്റെ വികർണ്ണം കൊണ്ടു പ്രതിനിധീകരിയ്ക്കാം.

അതുപോലെ.

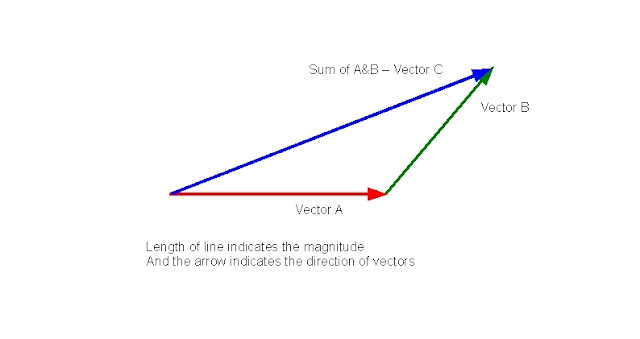
ബലങ്ങളെ ഒരു ത്രികോണത്തിന്റെ വശങ്ങളായി വരയ്ക്കാൻ കഴിയുമെങ്കിൽ അവയുടെ തുകയെ ആ ത്രികോണത്തിന്റെ മൂന്നാമത്തെ വശം പ്രതിനിധീകരിയ്ക്കും.

ഈ നിയമങ്ങൾ എല്ലാ വെക്ടറുകൾക്കും പ്രയോഗിയ്ക്കാം.

ഇപ്രകാരം ഗ്രാഫ്‌ ചിത്ര സങ്കേതമുപയോഗിച്ചു വെക്ടറുകളെ പ്രതിനിധീകരിയ്ക്കാനും അവയുടെ സങ്കലനം ( Addition ) നടത്താനും സാധിയ്ക്കും എന്നു മനസ്സിലായി.

2, ഗണിതപരമായ പ്രതിനിധീകരണം. ( Mathematical representation )

സാധാരണ ഗണിതക്രിയകളിൽ നമ്മൾ അളവുകളെ A,B,C മുതലായ അക്ഷരങ്ങളുപയോഗിച്ചു എഴുതും. ഉദാഹരണത്തിനു ഒരു വടിയുടെ നീളം A മീറ്റർ എന്നിരിയ്ക്കട്ടെ എന്നൊക്കെ കണക്കുകളിൽ സൗകര്യത്തിനുപയോഗിയ്ക്കാറുണ്ട്‌. ഇങ്ങനെ എഴുതുമ്പോൾ  അത്‌ വെക്ടറാണോ സ്കൈലറാണോ എന്നു വ്യക്തമാക്കേണ്ടതുണ്ട്‌. അതിനായി ഇങ്ങനെ എഴുതുമ്പോൾ വെക്ടർ അളവുകളാണെങ്കിൽ അക്ഷരങ്ങളുടെ മുകളിൽ ഒരു അസ്ത്ര ചിഹ്നം ( Arrow mark)  ചേർക്കും.

ഇതു വായിയ്ക്കുമ്പോൽ വെക്ടർ  A  എന്നു വായിയ്ക്കും.

ഇങ്ങനെ എഴുതിയാലും അവയെ ഗണിതക്രിയയിലുപയോഗിയ്ക്കുമ്പോൾ അവയുടെ മൂല്യവും ദിശയും വേണ്ടിവരുമെന്നറിയാമല്ലോ.. അതു ഗ്രാഫിക്കലായി എങ്ങനെ ചെയ്യാമെന്നു നാം കണ്ടു. ഗ്രാഫിക്കലായുള്ള പ്രതിനിധീകരണവും ഗണിതപരമായ പ്രതിനിധീകരണവും യഥാർത്ഥത്തിൽ ഒന്നു തന്നെയാണ്‌. ഗണിതപരമായിട്ടാണെങ്കിൽ അതിനു വിവിധ മാർഗ്ഗങ്ങളുണ്ട്‌. അവ താഴെക്കൊടുക്കുന്നു

1, ചതുർഭുജ ഘടക രീതി ( Rectangular components or complex form)

2, ധ്രുവീയ രീതി ( Polar form )

3, ത്രികോണമിതി രീതി ( Trignometric form )

4, വൃദ്ധി സംജ്ഞാ രീതി ( Exponential form )

1  ചതുർഭുജ ഘടക രീതി ( Rectangular components or complex form )

 ഈ രീതിയിൽ വെക്ടറിനെ ഘടകങ്ങളാക്കി  ഘടകങ്ങളെ ( Components) ഒരു ചതുർഭുജത്തിന്റെ സമീപ വശങ്ങളാക്കി എഴുതുന്നു. ചിത്രം ശ്രദ്ധിയ്ക്കുക.

 ഗ്രാഫിൽ നമ്മുടെ വെക്ടറിനെ വരച്ചിരിയ്ക്കുന്നു. “Ø“ എന്നടയാളപ്പെടുത്തിയിരിയ്ക്കുന്നത്‌ X അക്ഷത്തിൽ നിന്നുള്ള അതിന്റെ കോണീയ ദിശയാണ്‌. ഈ വെക്ടരിനെ രണ്ടു ഘടകങ്ങളാക്കി ഈ ഗ്രാഫിൽ തെന്നെ രേഖപെടുത്താം. ചിത്രം ശ്രദ്ധിയ്ക്കുക 

Y അക്ഷത്തിലും X അക്ഷത്തിലുമായു രണ്ടു ഘടകങ്ങളാക്കി വെക്ടറിനെ പിരിച്ചിരിയ്ക്കുന്നു. X  ലെ ഘടകത്തിനെ “a” എന്നും Y ലെ ഘടകത്തിനെ ”b” എന്നും രേഖപ്പെടുത്തിയിരിയ്ക്കുന്നു. നമ്മുടെ വെക്ടർ ” A ” യെ ”a” എന്നും “b” യെന്നുമുള്ള രണ്ടു ഘടകങ്ങളാക്കി എഴുതാം . ഇതു “a+ jb” എന്നാണെഴുതുന്നത്‌

ഇവിടെ ”b”  യുടെ കൂടെ” j” എന്നു ചേർത്തിട്ടുണ്ട്‌ അതിനർത്ഥം ”b”   എന്ന ഘടകം X അക്ഷത്തിൽ നിന്നും 90⁰ ഇടത്താണെന്നാണ്‌ (അപ്രദക്ഷിണ ദിശ-Anticlockwise direction) . “a”  യുടെ കൂടെ “j” ഇല്ല അതു സൂചിപ്പിയ്ക്കുന്നത്‌ “a” എക്സ്‌ അക്ഷത്തിലാണെന്നുമാണ്‌.

Horizontal component or real component a = Acosø

Horizontal component or imaginary component b =A sinø

A= √(a²+jb²)

“J”

ഇതിനെ സാധാരണ “+, -, X, ÷  മുതലായ അങ്കഗണിത പ്രവർത്തകങ്ങളെപ്പോലെ ( Arithametic operators ) ഒരു പ്രവർത്തകമായാണു പരിഗണിയ്ക്കുന്നത്‌. ഗണിതശാസ്ത്രത്തിൽ “j” യ്ക്കു പകര “i" ഉപയോഗിയ്ക്കും വൈദ്യുത ശാസ്ത്രത്തിൽ “i"  എന്നത്‌ പ്രവാഹതീവ്രതയുടെ ചിഹ്നമായി പരിഗണിയ്ക്കുന്നതിനാൽ രണ്ടും കൂടികലർന്നു ആശയക്കുഴപ്പമുണ്ടാകാതിരിയ്ക്കാനായി “i" യ്ക്കു പകരം “j” ഉപയോഗിയ്ക്കുന്നു.

“j” ഉടെ മൂല്യം √-1ആൺ`.  “j” കൊണ്ടു ഗുണിച്ചാൽ വെക്ടറിനു 90 ഡിഗ്രി ഇടത്തോട്ടു കോണീയ സ്ഥാനന്തരമുണ്ടാകും (angular displacement),

വെക്ടറുകളുടെ സങ്കലനവും വ്യവകലനവും ചതുർഭുജ ഘടക രീതിയിൽ.

വെക്ടറുകളുടെ സങ്കലനവും വ്യവകലനവും ഈ രീതിയിൽ വളരെ എളുപ്പമാണ്‌ താഴെ നോക്കുക.

വെക്ടർ A, വെക്റ്റർ B എന്നിവ തമ്മിൽ കൂട്ടണം എന്നു കരുതുക. അതിനേ അവയുടെ X അക്ഷത്തിലെ ഘടകങ്ങളെ തമ്മിലും, Y അക്ഷത്തിലെ ഘടകങ്ങളെ തമ്മിലും കൂട്ടിയാൽ മതി. അപ്പോൽ സങ്കലനം ചെയ്തു കിട്ടിയ മൂന്നാമത്തെ വെക്ടറിന്റെ ഘടകങ്ങളെ കിട്ടും. കൂട്ടിച്ചേർത്താൽ മൂന്നാമത്തെ വെക്ടറിന്റെ മൂല്യം  കോണീയ ദിശ എന്നിവയും കിട്ടുന്നതാണ്‌. താഴെ നോക്കുക.

വെക്ടർ A യെ a+jb എന്നെഴുതാം

വെക്ടർ B  ആകട്ടെ a1+jb1 എന്നും എഴുതാം. അവതമ്മിൽ കൂട്ടുമ്പോൾ X അക്ഷത്തിലെ ഘടകങ്ങളായ a യും a1 തമ്മിൽ കൂട്ടുന്നു, Y അക്ഷത്തിലെ ഘടകങ്ങളായ b യും b1 തമ്മിലും കൂട്ടുന്നു. അപ്പോൽ മൂന്നാമതു കിട്ടുന്ന വെക്ടറിന്റെ x ഘടകം = a+a1 ഉം, y ഘടകം b+b1 ഉം ആകും. പുതിയ വെക്ടറിന്റെ x ഘടകത്തെ a2 എന്നും Y ഘടകത്തെ b2 എന്നും എഴുതിയാൽ

a₂=a+a₁,

b₂=b+b₁ ഉം ആകും. ആ വെക്ടറിനെ a₂+jb₂ എന്നെഴുതാം. തുക കൂട്ടി കിട്ടുന്ന വെക്ടറിന്റെ മൂല്യം കാണുന്നതിനെ √(a₂)²+(b₂)² എന്നു ചെയ്താൽ മതിയാകും

പുതിയ വെക്ടറിന്റെ കോണീയ സ്ഥാനം (ദിശ) കാണുന്നതിന്‌ tan_1 (b₂/a₂ ) ചെയ്താൽ മതി.

വെക്ടറുകളെ തമ്മിൽ വ്യവകലനം ചെയ്യുന്നതിന്‌

അതത് ഘടകങ്ങളെ കൂട്ടുന്നതിനു പകരം തമ്മിൽ കുറച്ചാൽ മതി. ബാക്കിയെല്ലാം സങ്കലനം പോലെ തന്നെ.

a2=a-a1,

b2=b-b1

വെക്ടറുകളെ തമ്മിൽ വ്യവകലനം സങ്കലനം എന്നിവയ്ക്കാണ്‌  ഈ രീതി എളുപ്പമാകുക. ഗുണനത്തിനും ഹരണത്തിനും ഈ രീതി വളരെ സങ്കീർണ്ണമാണ്‌. അതിനായി exponential രീതിയോ polar രീതിയോ ആണ്‌ എളുപ്പം

2, ധ്രുവീയ രീതി ( Polar form )

ഈ രീതിയിൽ വെക്റ്ററിന്റെ മൂല്യത്തോടൊപ്പം അതിന്റെ ദിശയും രേഖപ്പെടുത്തിയിട്ടുണ്ട്. X അക്ഷത്തിൽ നിന്നുള്ള കോണീയ അകലത്തിന്റെ രൂപത്തിലാണതു രേഖപ്പെടുത്തുക. വെക്ടറിന്റെ മൂല്യം A യും ദിശ 30 ഡിഗ്രിയുമാണെങ്കിൽ വെക്ടറിനെ A∟30⁰എന്നിങ്ങനെ രേഖപ്പെടുത്താം

വെക്ടറുകളുടെ ഗുണനം

വെക്ടറുകൾ ഈ രീതിയിൽ ഗുണിയ്ക്കുന്നതിനായി മൂല്യങ്ങൾ പരസ്പർം ഗുണിയ്ക്കുക. കോണീയ അലവുകൾ പരസ്പരം കൂട്ടുക. അപ്പോൾ ഗുണനഫലത്തിന്റെ മൂല്യവും ദിശയും കിട്ടും താഴെ നോക്കുക.

വെക്ടർ A - A∟30⁰

വെക്ടർ B - B∟20⁰

വെക്ടർ A x  വെക്ടർ B = A X B ∟30+20

എന്നു കിട്ടും.

ഹരിയ്ക്കുന്നതിനു മൂല്യങ്ങൾ തമ്മിൽ ഹരിച്ച് ശേഷം കോണളവുകൾ തമ്മിൽ കുറച്ചാൽ മതി.

3, ത്രികോണമിതി രീതി ( Trignometric form )

ഈ രീതിയിൽ വെക്ടറിനെ  ത്രിഗോണമിതി ഘടകങ്ങളായി പിരിച്ചെഴുതുന്നു. താഴെ നോക്കുക. ഇത് complex form നു സമാനമാണ്‌

വെക്ടർ A= Acosø+A sinØ

=A(cosø+sinø)

കോണുകൾ അളക്കുന്ന രീതി

റഫറൻസായി കണക്കാക്കുന്ന അക്ഷത്തിൽ നിന്നും അപ്രദക്ഷിണ ദിശയിലാണ്‌ (anticlockwise direction) കോണുകൾ അളക്കുന്നതെങ്കിൽ അത് നെഗറ്റീവായും, പ്രദക്ഷിണ ദിശയിലാണെങ്കിൽ (Clockwise direction) പോസിറ്റീവ് ആയും കണക്കാക്കും. താഴെ നോക്കുക.

4, വൃദ്ധി സംജ്ഞാ രീതി ( Exponential form )

ഈ രീതിയിൽ താഴെക്കാണും വിധം വെക്ടറുകളെ പ്രതിനിധീകരിയ്ക്കാം

Vector A = Ae^jø

വെക്ടറുകളെ ഏതുരീതിയിൽ നിന്നും മറ്റു രീതിയിലേയ്ക്കൂ സൗകര്യാർത്ഥം പരിവർത്തനം ചെയ്യാം

ഫേസർ (phasor)

നിശ്ചിതമായ അക്ഷത്തെ അപേക്ഷിച്ച് കറങ്ങിക്കൊണ്ടിരിയ്ക്കുന്ന വെക്ടറുകളെയാണ്‌ (rotating vectors) ഫേസറുകൾ എന്നു പറയുന്നത്. ആൾടർനേറ്റിങ്ങ് ഇലക്ട്രിക് കറണ്ട്, ആൾട്ടർനേറ്റിങ്ങ് വോൾട്ടേജ് (AC current and voltage) എന്നിവയെ ഫേസറുകളായി കണക്കാക്കാം. ഫേസറുകളെല്ലാം അപ്രദിക്ഷിണ ദിശയിൽ കറങ്ങുന്നതായി സങ്കല്പിയ്ക്കുന്നു. അവയെ ഗ്രാഫിയ്ക്കലായി താഴെ ക്കാണും വിധം പ്രതിനിധീകരിയ്ക്കാം. ഇതിലെ രശ്മിയുടെ നീളം ഫേസറിന്റെ rms മൂല്യത്തേയും, X അക്ഷത്തിൽ നിന്നുള്ള കോണീയ അകലം അതിന്റെ തൽസമയ ദിശയേയും പ്രതിനിധീകരിയ്ക്കും

ഫേസ് 

ഒരു ആൾടർനേറ്റിങ്ങ് ക്വാണ്ടിറ്റി (ഫേസർ) റഫറൻസ് അക്ഷത്തിൽ നിന്നും എത്ര ദൂരത്തിലാണ്‌ എന്നു പ്രസ്താവിയ്ക്കുന്നതാണ്‌ അതിന്റെ ഫേസ്. ഫേസറുകൾ ഒരു നിശ്ചിത വേഗതയിൽ ഒരു ബിന്ദുവിനെ ആസ്പദമാക്കി കറങ്ങുകയാണെന്നു പറഞ്ഞല്ലോ. ആ വേഗതയെ കോണീയ പ്രവേഗമെന്നു (angular velocity) പറയും. കോണീയ പ്രവേഗമെന്നത് യൂണിറ്റ് സമയത്തിനുള്ളിൽ ഫേസറിനുണ്ടാകുന്ന കോണീയ സ്ഥാനാന്തരണമാണ്‌ (angular displacement). ഉദാഹരണത്തിനെ ഒരു ഫേസർ ഒരു സെക്കന്റ് കൊണ്ട് 360 ഡിഗ്രി പിന്നിടുന്നെങ്കിൽ അതിന്റെ കോണീയ പ്രവേഗം 3600/സെക്കന്റ് ആണ്‌. കോണീയ പ്രവേഗത്തെ “ω” എന്ന ചിഹ്ന്നം കൊണ്ടു പ്രതിനിധീകരിയ്ക്കും. ഫേസിനെ കോണീയ അകലം കൊണ്ട് സൂചിപ്പിയ്ക്കാം, അല്ലെങ്കിൽ സമയം കൊണ്ടു സൂചിപ്പിയ്ക്കാം. ഉദാഹരണത്തിന്‌ ചിത്രത്തിലെ ഫേസറിന്റെ ഫേസ് 30 ഡിഗ്രിയാണെന്നു പറയാം, അല്ലേങ്കിൽ 1/12 സെക്കന്റെന്നും പറയാം. കോണളവിൽ പറയുന്നതാണ്‌ ഗണിതക്രിയകൾക്കു സൗകര്യം.

ഫേസ് വ്യത്യാസം.

ആദ്യമേ അളവുകളുടെ കാര്യം പറഞ്ഞതുപോലെ ഫേസും ഒറ്റപ്പെട്ടു നില്ക്കുന്ന ഒരു സംഗതിയല്ല. ഒരു റെഫറൻസിൽ നിന്നുമാണതും അളക്കാനാകുക. റെഫറൻസിനെ പൂജ്യമായി കണക്കാക്കുമെന്നു മാത്രം. ഒന്നിലധികം ഫേസറുകൾ ഒരു ഘടകത്തിൽ ബാധകമാകുമ്പോൾ പൂജ്യം രഫറൻസിൽ നിന്നവയോരോന്നിന്റേയും ഫേസ് കണക്കാക്കുന്നതിനേക്കളെളുപ്പം ഫേസറുകൾ തമ്മിലുള്ള കോണീയ അകലം കണക്കാക്കുന്നതാണ്‌. ഇതിനെ ഫേസ് വ്യത്യാസം എന്നു പറയും, കൂടുതൽ മനസ്സിലാകാനായി താഴത്തെ ചിത്രങ്ങൾ നോക്കുക.

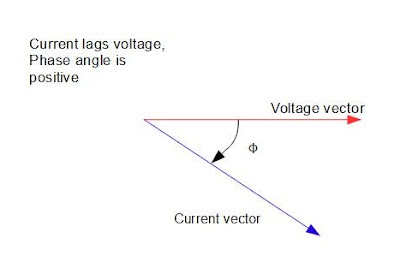
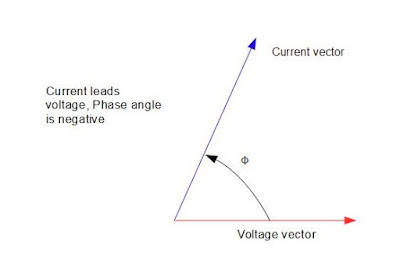
വോൾട്ടേജും കറണ്ടും തമ്മിൽ ഒരു പരിപഥത്തിൽ പരിഗണിയ്ക്കുമ്പോൾ അവതമ്മിലുള്ള കോണീയ അകലത്തെ ഫേസ് ആംഗിൾ എന്നു പറയും. ഈ ഫേസ് ആംഗിൾ ആണ്‌ വോൾട്ടേജും കറണ്ടും തമ്മിലുള്ള ഫേസ് വ്യത്യാസം. വോൾട്ടേജിന്റെ പിന്നിലാണ്‌ (പ്രദക്ഷിണദിശയിൽ) കറണ്ട് വെക്ടറെങ്കിൽ

കറണ്ട് വോൾട്ടേജിനെ ലാഗ് (lag) ചെയ്യുന്നുവെന്നും മറിച്ചാണെങ്കിൽ ലീഡ് (lead) ചെയ്യുന്നെന്നും പറയും